A Right Circular Cylinder Is Inscribed in a Cone

A right circular cylinder is inscribed in a cone with height h and base radius r Find the largest possible volume of such a cylinder. Given any right circular cone with a right circular cylinder inscribed inside it what percent of the volume of the cone does such a.

Solved A Cylinder Is Inscribed In A Right Circular Cone Of Chegg Com

A cylinder is inscribed in a right circular cone of height 4 and radius at the base equal to 6.

. Find the largest possible volume of such a cylinder. A right circular cylinder is inscribed in a cone with height 6m and radius 3m. I Find the Surface Area S of the circular cylinder as a function of x.

Find the radius of the cylinder. What are the dimensions of such a cylinder which has maximum volume. Let R and H be the radius and height of the cone and let r and h be the radius and height of the cylinder.

Find the maximum volume of right circular cylinder that can be inscribed in a cone of altitude 12 cm and base radius 4 cm if the axes of the cylinder and con coincide. To ask Unlimited Maths doubts download Doubtnut from - httpsgoogl9WZjCW A right circular cylinder is inscribed in a cone. Ii Find a relation connecting x and R when S is a maximum.

The relationship between r and h and R and H is given by rR H-hH so solving for r gives r RH-hH. Answer pi h x2-pi h r x3pi h x21-x rpileftfrac23 rright2 hleft1-frac23rightfrac427 pi r2 h. A right circular cylinder is inscribed inside a cone.

A right circular cylinder is inscribed in a given cone of radius R cm and height H cm as shown in the figure. The curved surface area is maximum. The cone has diameter and altitude and the axes of the cylinder and cone coincide.

A right circular cylinder is inscribed in a cone with height h and base radius r. From the diagram the radius of the inscribed cylinder is r 5 x. The volume of the cylinder is V pi r2 h.

Arrow_forward A grain silo has the shape of a right circular cylinder surmounted by a hemisphere. A right circular cylinder is inscribed in a cone with height h and base radius r. S Curved Surface Area of Cylinder.

H 1 be the height of the cone. Height of cylinder E inches. The problem is Im currently out of town and the teacher is out of office.

R be the radius of the inscribed cylinder. Find the largest possible volumeofsuchacone1 At right are four sketches of various cylinders in-scribed a cone of height h and radius r. Let us consider r 1 be the radius of the cone.

A right circular cylinder with its diameter equal to its height is inscribed in a right circular cone. The diagram below shows x. For every five units we move to the right we go up 6 units.

Find the largest possible volume of such a cylinder. Radius of cone is any of the line segments from its center to its perimeter and in more modern usage it is also their length. A given right circular cone has a volume p and the largest right circular cylinder that can be inscribed in the cone has a volume q.

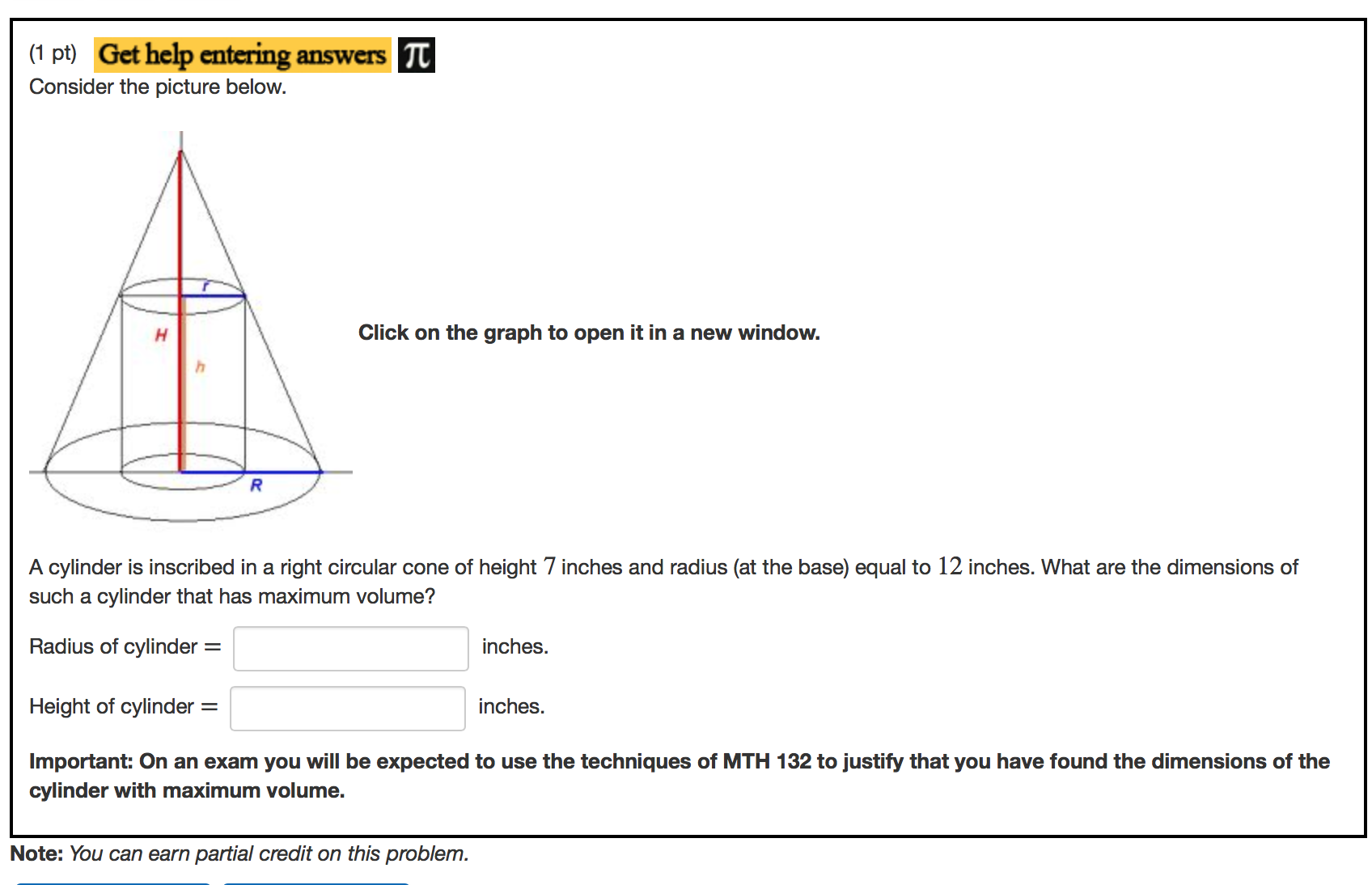
H R Click on the graph to open it in a new window. Radius of cylinder inches. Find the largest volume V of the circular cone that can be inscribed in a sphere of radius 10 cm.

Show that the curved surface. A cylinder is inscribed in a right circular cone of height 9 inches and radius at the base equal to 10 inches. How fast is the height of the pile.

From these sketches it seems that the volume of the cylin-der changes as a function of the cylinders radius x. The volume of largest right circular cylinder that can be inscribed within cone is the quantity of three-dimensional space enclosed by a closed surface and is represented as V 8 pi R 2 H 27 or Volume 8 pi Radius of cone 2 Height of Cone 27. Find the dimensions of the right circular cylinder of maximum volume that can be inscribed in a right circular cone of radius R and altitude H Relevant Equations.

It forms a pile in the shape of a right circular cone whose base diameter and height are always the same. Interact with this applet for a few minutes. Slope rise run 6 5.

DF r and AD AL DL h 1 h. The height of the cylinder of maximum curved surface area that can be inscribed in a sphere of radius R is. A right circular cylinder is inscribed in a cone.

Answer 1 of 3. H be the height of the inscribed cylinder. What are the dimensions of such a cylinder that has maximum volume.

A right circular cylinder is inscribed in a cone with height h and base radius r. A cylinder is inscribed in a right circular cone of height 65 and radius at the base equal to 55. A right circular cylinder is inscribed in a right circular cone with an altitude of 12cm and radius of base is 5cm.

Based on the above information answer the following questions. Thus V pi RH-h. Find the radius and height of the right circular cylinder of the largest volume that can be inscribed in a right circular cone with a radius of 6 inches and height of 10 inches.

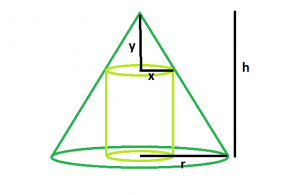
Find step-by-step Calculus solutions and your answer to the following textbook question. The applet below shows a right circular cylinder inscribed inside a right circular cone. Y 6 5 x.

We can also express the height of the cylinder y in terms of x because we know the slope of the slanted side of the cone. What are the dimensions of such a cylinder which has maximum volume.

Optimization Of Cylinder Inscribed In Cone Maximum Volume And Surface Area Youtube

A Right Circular Cylinder Is Inscribed In A Cone Show That The Curved Surface Area Of The Cy Youtube

Largest Right Circular Cylinder That Can Be Inscribed Within A Cone Geeksforgeeks